Diffie-hellman Calculator
Diffie Hellman Algorithm (DH) Diffie Hellman (DH) key exchange algorithm is a method for securely exchanging cryptographic keys over a public communications channel. Keys are not actually exchanged – they are jointly derived. It is named after their inventors Whitfield Diffie and Martin Hellman. The Diffie-Hellman key exchange uses a large prime pand a primitive root gof this prime. These numbers are both public. To start the key exchange process, Alice chooses a secret number aless than the large prime, and computes ga(mod p). Alice sends this answer, call it A, to Bob.
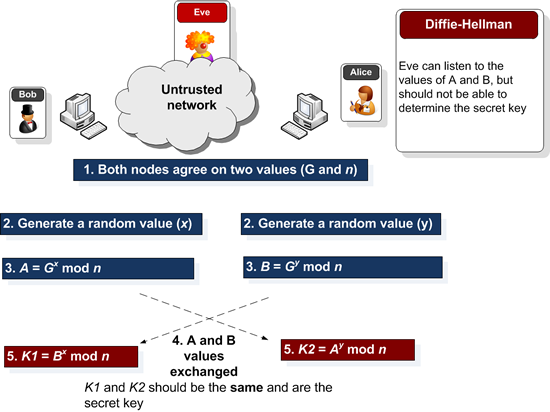
[Back] Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications, and uses two numbers (G and N) for the first part of the calculation (of which N must be a prime number):
[Related Lecture] [Tutorial] [Software Tutorial][Software Lecture] [Theory][Blog] [Picking G value] Next Bob and Alice will generate two random numbers (X and Y), calculate an X value and a Y value, respectively:
| Bob's X Value | Alice's Y value |
| Bob's random value | Alice's random value |
| Bob's A value | Alice's B value |
| A=G^x mod N | B=G^y mod N |
Diffie-hellman Calculator
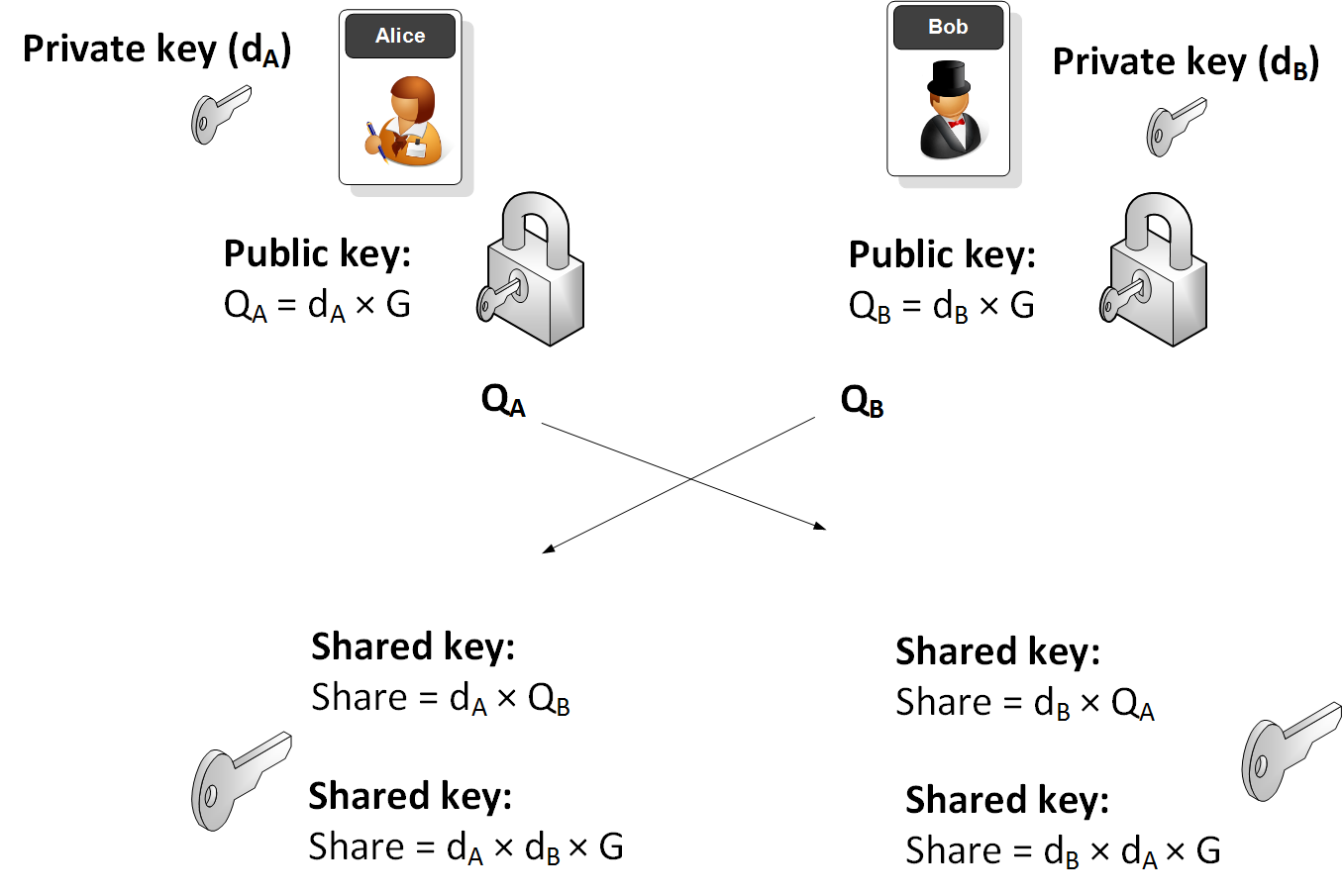
The Elliptic-Curve Diffie–Hellman (ECDH) is an anonymous key agreement protocol that allows two parties, each having an elliptic-curve public–private key pair, to establish a shared secret over an insecure channel.
and Bob will send his A value to Alice, and Alice will send her B value to Bob, and they now re-calculate the values to generate the same shared key:
| Bob's Key | Alice's Key |
| Key=B^x mod N | Key=A^y mod N |